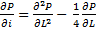
Босс осудит их одного за другим, и Сильвана должна быть побеждена, прежде чем она применит Массивное разрушение 4 раза. Оффтанк должен наступить на лужи на земле, затем переместиться в угол платформы, а затем рассеяться, чтобы разместить их в наилучшем возможном месте на платформе.
Тогда как получить Diablo Hearthstone? Как получить Diablo в Hearthstone Battlegrounds Diablo предлагается игрокам случайным образом в каждом лобби. Есть шанс, что вы будете выбраны, но если нет, то кто-то из вашего лобби, скорее всего, получит это.
Как работает поле битвы в Hearthstone? Поле битвы является одним из трех основных режимов игры вHearthstone. Вы сталкиваетесь с 7 другими игроками в Батай эпично, используя миньонов, которых вы набираете и улучшаете в течение раундов. Одержите победу, победив всех своих противников.
🔥ВСЕ ПРО 3 СЕЗОН В ПОЛЯХ СРАЖЕНИЯХ: НЕЖИТЬ, ДВОЙНЫЕ ТИПЫ СУЩЕСТВ, НОВЫЙ ГЕРОЙ, ИЗМЕНЕНИЕ СТАРЫХ
Как получить крылья Diablo Immortal?
КОММЕНТАРИЙ получать Ailes в Diablo Бессмертный
Как только вы достигнете 1 резонанса, вы можете автоматически получить Ailes 1-й уровень. Ailes появится в меню косметики, как только вы достигнете необходимого количества резонанса.
Как играть в Карнифлору?
Советы и рекомендации по игре в Carniflore Лучше побеждать в дуэлях и иметь прочную доску. Если вы быстро получите Охотника на кроликов, начните стратегию вокруг этой карты. Другие игроки вряд ли бросятся на это, и вы можете извлечь из этого максимум пользы.
Как играть за танцора Дэрила?
Игра с танцором Дэрилом В начале игры найдите миньона, которого хотите усилить, купите всех остальных миньонов в таверне и затем продайте их. Когда вы улучшите свою таверну и найдете полезных миньонов для поздней игры, сохраните их.
Как играть с Юдорой?
Юдора — маг, для разблокировки которого требуется несколько боевых очков. Его заклинания позволяют ему наносить значительный групповой урон. Он идеальный персонаж для начала. Мы рекомендуем использовать набор снаряжения для непрерывного урона.
Какой легендарный ремесленник Hearthstone?
. легендарный от Разделенного в Альтеракской долине до выработать в приоритете
- Мастер теней Чак:
- Гафф Уайлдхарт:
- Обетрент Магистр:
- Озаренный Кариэль:
Каким классом играть в хартстоун?
Какой лучший класс в Hearthstone? Паладин остается лучшим классом арены, и был им с самого начала игры.Утер просто наделен лучшими существами в игре, помимо обладания очень мощными заклинаниями для управления противоборствующей доской.
Какую карту распылить в Hearthstone?
Золотые карты, с другой стороны, более дорогие с точки зрения чародейной пыли и поэтому являются очень хорошими целями для распыления.
Как крафтить карты Hearthstone?
Создание карты Когда вы распыляете чары, у вас будет достаточно пыли для создания карты. Чтобы создать ее, просто зайдите в свою коллекцию карт и отобразите «Все карты» в игре.
Эвелон Нанял Тренера по Хартстоуну за 500к / Сильвернейм учит Эвелона
Какой герой Hearthstone лучший?
Паладин остается лучшим классом арены, и был им с самого начала игры.Утер просто наделен лучшими существами в игре, помимо обладания очень мощными заклинаниями для управления противоборствующей доской. Новые весы чрезвычайно сильны в самообороне.
Какая колода хартстоуна?
Лучший палуб из сердца затонувшего города
- Шаманский ожог.
- Меха Маг.
- Друид Рамп.
- Пиратский вор.
- Знак охотника на демонов.
Как сделать хорошую колоду для арены в Hearthstone?
Собирая наши карты, мы должны держать в поле зрения нашу кривую маны. В колоде могут быть очень хорошие карты, но если кривая маны слишком высока, она будет просто уничтожена любым игроком, имеющим «хороший» выход из-за слишком слабых первых ходов.
Когда следующее дополнение для Hearthstone?
Blizzard назначает игрокам встречу 27 июня 2022 года для первых откровений относительно этого будущего. расширение ! Не стесняйтесь делать свои прогнозы благодаря видео, которое вы найдете в оставшейся части этой статьи.
Когда заканчивается сезон Hearthstone?
Hearthstone Grandmasters завершится двумя последними сезонами в 2022 году. В первом сезоне, который пройдет в феврале и марте следующего года, все 1 гроссмейстеров соревнуются в течение короткого четырехнедельного сезона.
Почему Hearthstone не работает?
Убедитесь, что ваше устройство соответствует или превышает минимальные требования для запуска Hearthstone. Только для устройств Android: очистите кеш приложения Hearthstone («Настройки» > «Приложения» > Hearthstone > «Очистить все данные кеша»).
Каким классом играть в Hearthstone?
Какой лучший класс в Hearthstone? Паладин остается лучшим классом арены, и был им с самого начала игры.Утер просто наделен лучшими существами в игре, помимо обладания очень мощными заклинаниями для управления противоборствующей доской.
Как учиться в Hearthstone?
Если вы хотите продолжить свое обучение против искусственного интеллекта, мы советуем вам принять участие в бесплатных приключениях. Один из них, Пепел Запределья, позволяет восстановить многие карты, используемые в колоде Охотника на демонов.
Как войти в Hearthstone?
Если вы попытались войти в Hearthstone на своем мобильном устройстве, используя аутентификацию Facebook, вам нужно будет завершить вход через Facebook, прежде чем вы сможете войти, используя свой адрес электронной почты Battle.net. Попробуйте сбросить пароль учетной записи Battle.net.
Как выиграть в хартстоун?
Несколько советов для начала Hearthstone
- Определите тему. …
- Запланируйте от 5 до 10 карт для начала игры. …
- Запланируйте от 5 до 10 карт на конец игры. …
- Отдайте предпочтение миньонам. …
- Со временем улучшайте свою колоду. …
- Вступайте в бой с недорогими миньонами.
Как заработать награды в Hearthstone?
Сражайтесь в одиночку за награды или бросайте вызов другим игрокам в боевых ямах! Нанимайте наемников, чтобы создать идеальную группу и извлечь выгоду из новых синергий. Благодаря постоянному прогрессу ваши наемники будут становиться сильнее по мере прохождения игрового режима.
Как играть классом в Hearthstone?
В меню режима игры у вас есть выбор между двумя разными баннерами. Один для игры в «рейтинговом» режиме, обозначенном медалью в виде разъяренного цыпленка (уровень, с которого начинает каждый игрок), а другой, представленный солнцем, для игр без рейтинга.
Что такое награда в Hearthstone?
Выполнив задание, вы получите сундук, полный монет наемников! Монеты наемников позволяют вам получить определенного наемника или улучшить способности и снаряжение этого наемника, если оно у вас уже есть.
Источник: sosordinateurs.com
Занимательная математика в Hearthstone
Я любитель популярной компьютерной карточной игры Hearthstone, разработанной компанией Blizzard Entertainment. Однажды я задался вопросом: «Можно ли исходя только из правил, описывающих динамику переходов игрока между уровнями при проигрышевыигрыше партии, получить статистику распределения игроков по достигнутому ими уровню?»
Несмотря на то, что в сети есть огромное количество сайтов и wiki, посвящённых Hearthstone, поверхностный поиск результатов не дал. На глубокий поиск было жаль времени, поэтому я решил задачу «на коленке». Полагаю, это решение может стать темой для занятия в школьном математическом кружке.
Описание задачи
- Уровни с 25 по 21 состоят из 2-х подуровней;
- Уровни с 20 по 16 состоят из 3-х подуровней;
- Уровни с 15 по 11 состоят из 4-х подуровней;
- Уровни с 10 по 1 состоят из 5-и подуровней;
- На «Легенде» подуровней нет.

Рисунок 1
Новый игрок стартует в рейтинге с 25-го уровня. За выигрыш партии игрок получает «звезду» (иногда – две), т.е. повышает свой подуровень на 1 (или 2 соответственно).
На линейке есть 4 диапазона, в которых отличаются правила изменения уровня игрока при выигрышепроигрыше партии:
Таблица 1
| «Трамплин» | 25-21 | Поражение: подуровень не меняется Победа: +1 3(и более) победы подряд: +2 |
| «Гонка с ускорением» | 20-6 | Поражение: -1 Победа: +1 3(и более) победы подряд: +2 |
| «Нормальная гонка» | 5-1 | Поражение: -1 Победа: +1 |
| «Легенда» | Легенда | Поражение: подуровень не меняется Победа: подуровень не меняется |
Очевидно, что «Трамплин» служит для Wowлечения новых игроков, так как на «трамплине» есть только награда, но нет наказания за поражение. Кроме того, понятно, что население «трамплина» экспоненциально быстро «вымирает», поскольку правила неизбежно выталкивают игрока с «трамплина» в диапазон «Гонки с ускорением». Вероятность остаться на «трамплине» после 18 игр составляет ~29%, а после 27 игр – менее 1,5%.
«Гонка с ускорением» помогает игрокам с высоким мастерством и хорошими колодами быстрее добраться до «Нормальной гонки», где и начинается настоящее «рубилово». Ну и, наконец, «Легенда» — загончик для топовых игроков.
- Вычислить вероятность получения игроком определённого уровня после определённого количества сыгранных игр;
- Вычислить распределение всех игроков по уровням в зависимости от времени.
Выбор метода решения и инструмента
Первой мыслью было написать программу на JS, моделирующую множество игроков, уровни которых в результате взаимодействия меняются по вышеприведённым правилам. По недолгом размышлении об объёме требуемого JS кода я решил, что электронные таблицы отлично подходят для решения этой задачи.
Идея решения следующая:
Пусть некоторый прямоугольный диапазон размером 96*1 (например диапазон Source!$C$3:$C$98 в прилагаемых файлах) представляет распределение количества игроков по линейке. Тогда, используя правила из таблицы 1, легко получить распределение, описывающее состояние, после того, как каждый игрок сыграл одну игру. Правила из таблицы 1 расположены в диапазоне Source!$D3:$D$98. Если «протащить» эти правила на нужное количество столбцов, то получившая таблица будет представлять изменение распределения игроков по уровням со «временем». Время в данном случае в кавычках потому, что здесь оно измеряется в «сыгранных играх».
Я начал с Open Office Calc, который всем хорош, но 3-D графики «из коробки» в нём выглядят убого (возможно, я просто не умею их готовить). В итоге решение реализовано на MS Excel и лежит здесь. Вариант для Open Office Calc там же — вполне функциональный, за исключением отсутствия 3-D графиков и отсутствия интерактивности в 2-D графиках.
Вероятность получения игроком определённого уровня
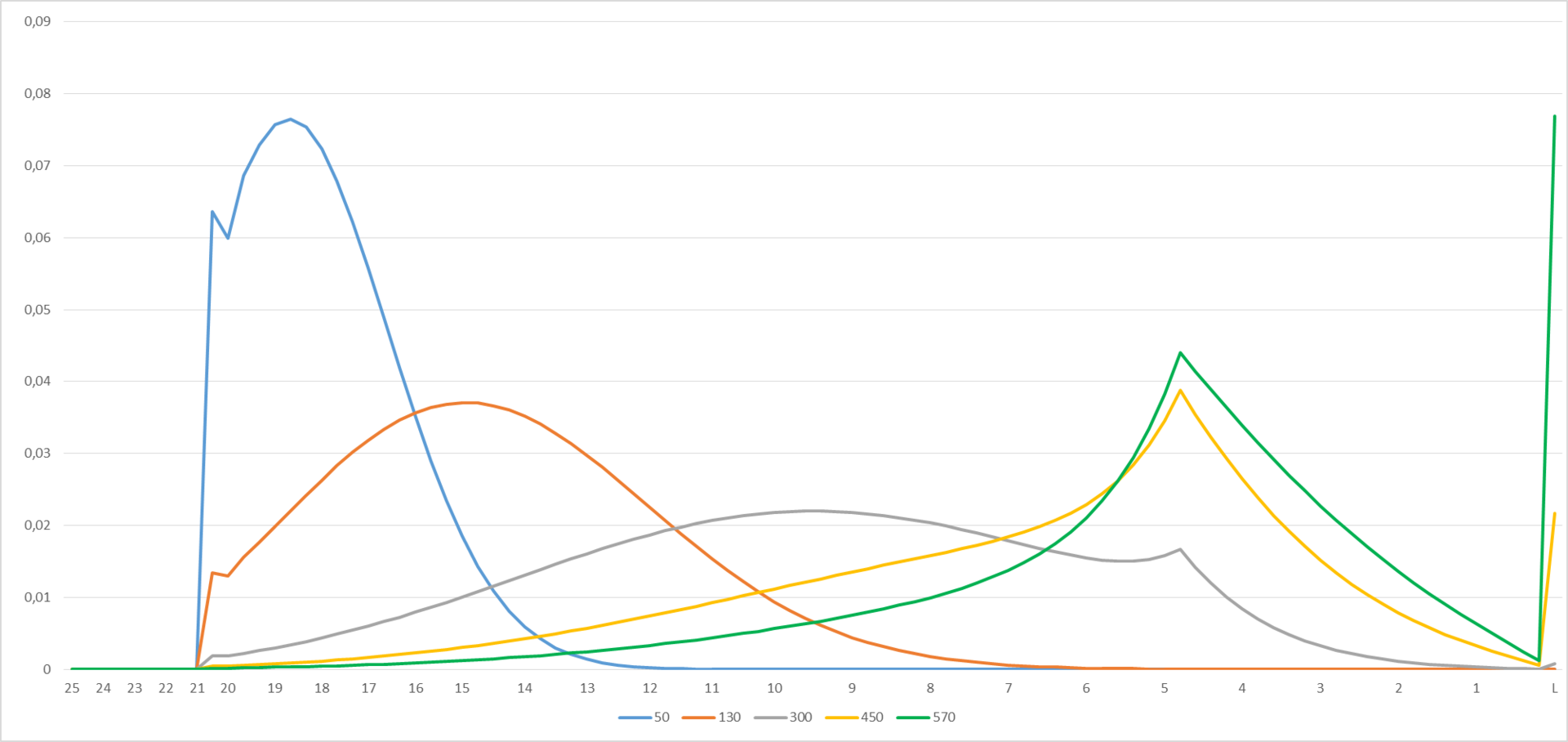
Рисунок 2
Приведённые графики описывают вероятность получить тот или иной уровень для игрока, стартовавшего с 25 уровня и сыгравшего 50, 130, 300, 450 или 570 игр соответственно. В Excel график интерактивный – можно поиграться с числами слева от диаграммы на вкладке «Interface», при этом графики (Рисунок 2) будут меняться.
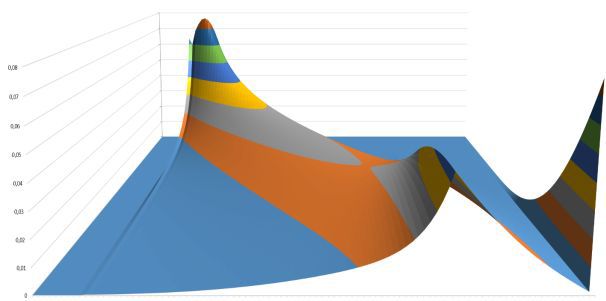
В 3-D эволюция вероятности получения определённого уровня выглядит очень симпатично:
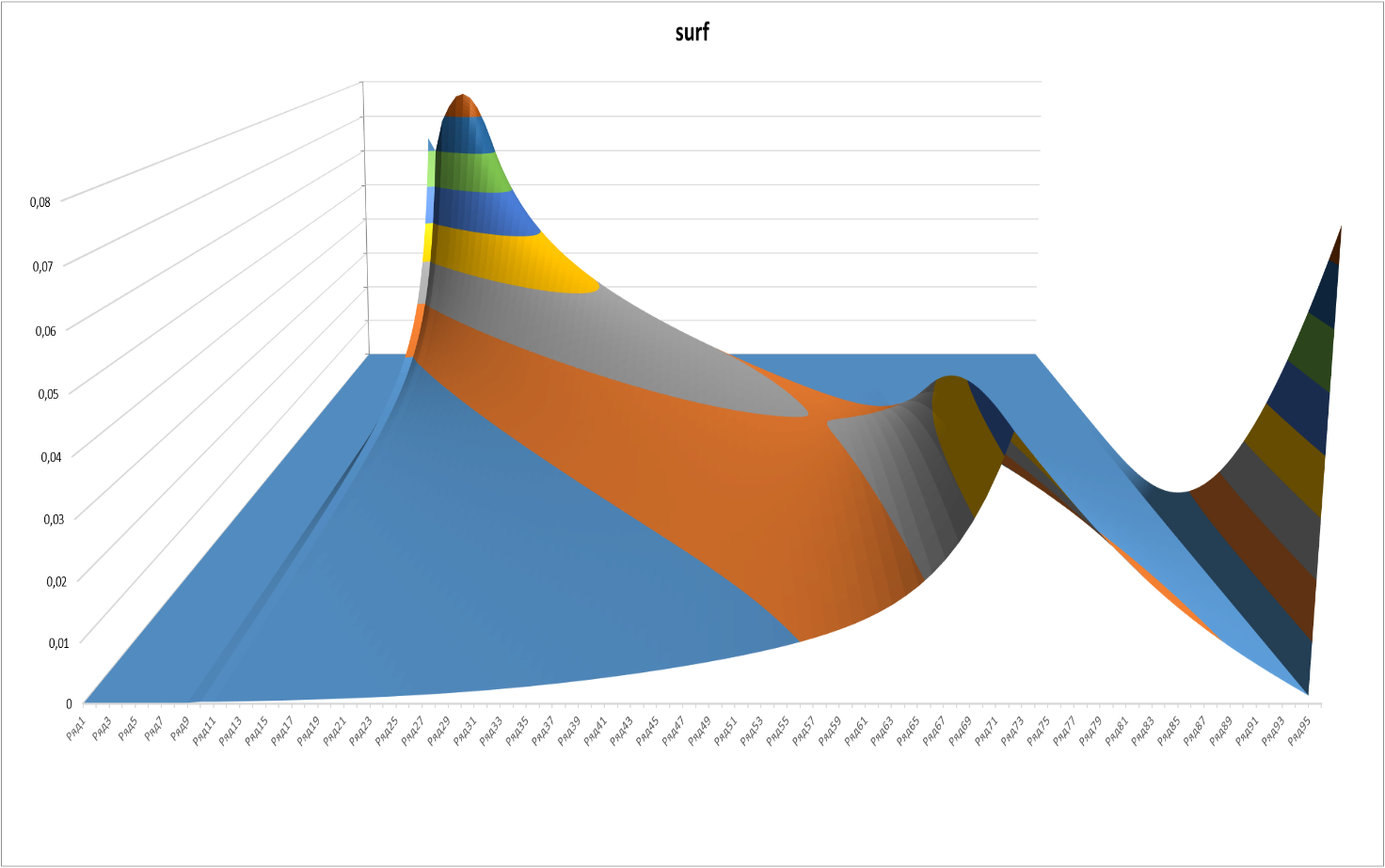
Рисунок 3
Здесь приведён срез с теми же минимальной и максимальной «временными» границами (50 и 570 игр), что и на рисунке 2.
Тот же график с другого ракурса:
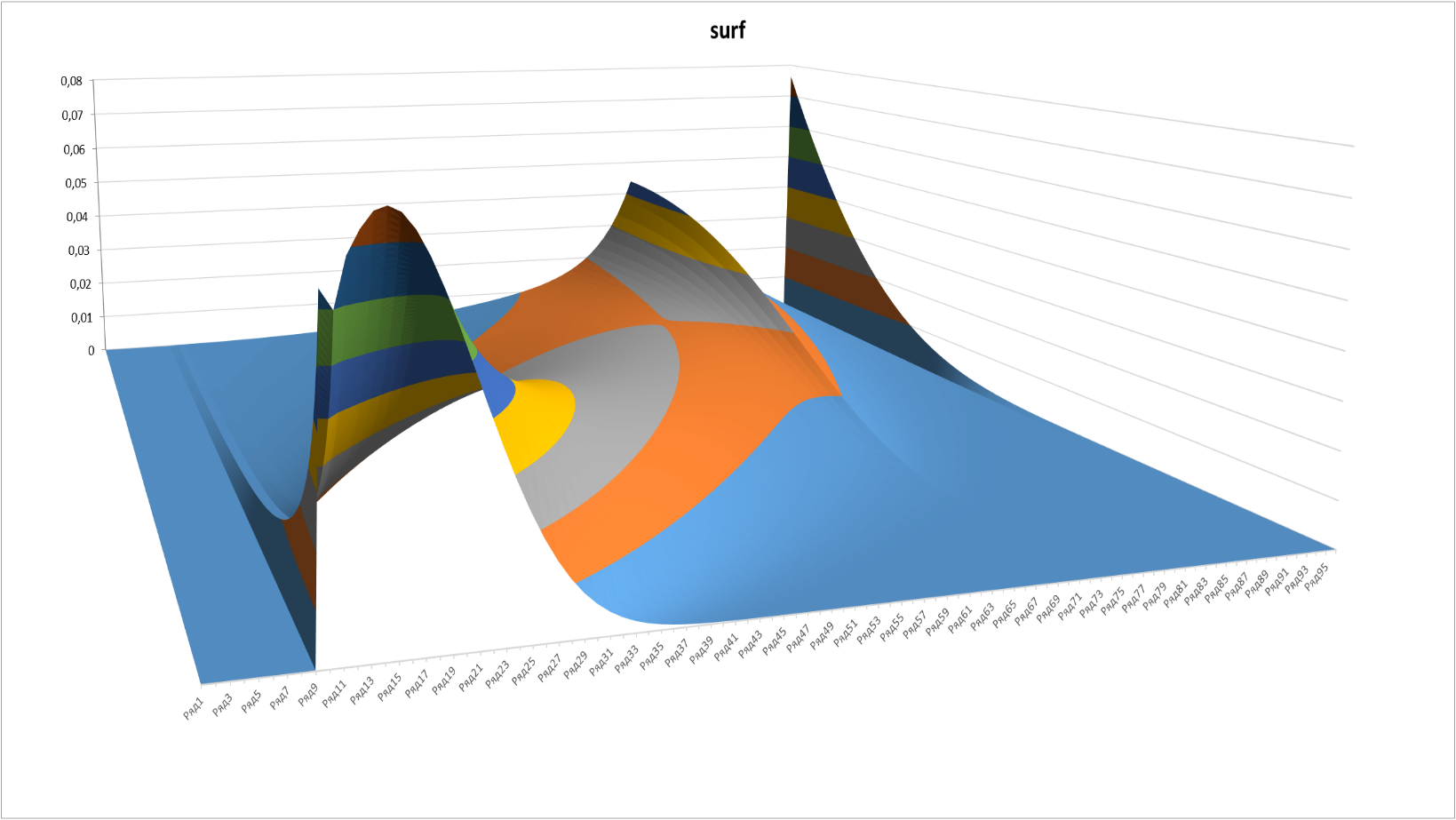
Рисунок 4
Несколько неожиданным выглядит появление «ребра» на графиках в точке, соответствующей уровню 5 и 2 «звезды» (72-й подуровень по порядку). Данная точка является последней, на которую действует возможность попадания «с ускорением» после 3+ побед подряд.
Если посмотреть правила для 71 – 72 подуровней, то они выглядят следующим образом:
71 =1/8*C69+C70*3/8+0,5*C72
72 =1/8*C70+C71*1/2+0,5*C73
Здесь СNN- количество игроков на подуровне NN на предыдущем шаге:
— первый член обеспечивает «ускоренный перенос» с уровня «текущий -2»;
— второй член обеспечивает обычный переход при победе на уровне «текущий -1»;
— третий член обеспечивает переход с вышележащего уровня при поражении.
Разница в 1/8 в коэффициенте при втором члене обусловлена тем, что, начиная с 5-го уровня (он же 71-й порядковый подуровень), независимо от числа побед подряд, повышение подуровня проходит только на 1, т.е. даже если победа на 71-м подуровне была для игрока 3-й, он перейдёт лишь на 72-й подуровень.
Эта небольшая на первый взгляд добавка приводит к тому, что «поток игроков» на 72-й подуровень чуть выше среднего, соответственно чуть выше будет и поток игроков с 72-го подуровня в его окрестности, т.е. эффект повышения потока игроков на 72-й подуровень самоусиливается, что и приводит к появлению этого замечательного ребра.
Вычисление распределения всех игроков по уровням
Очевидно, что игроки различаются по количеству игр, которые они играют за одно и то же время. Более увлечённые игроки играют больше, казуальные – меньше.
Для вычисления модельного распределения игроков по уровням необходимо знать функцию распределения игроков по количеству сыгранных ими игр.
Введём обозначения:
- P(L,i) ) — вероятность получения игроком определённого уровня (L) после заданного количества игр (i) (графики приведены на рисунках 2-4)
- N – максимальное количество игр, сыгранное самым увлечённым игроком. Заметим, что N здесь играет роль времени. Конечно, это не обычное время. Однако между обычным временем t и N есть следующее соотношение:
![]() , поэтому N в качестве «времени» вполне годится.
, поэтому N в качестве «времени» вполне годится. - Z (i, N) – вероятность того, что игрок сыграл i игр к моменту «времени» N или распределение игроков по количеству сыгранных игр за «время» N.
- D (L,N) – искомая вероятность нахождения игрока на уровне L, в момент «времени» N или распределение игроков по уровням на момент «времени» N.
Тогда 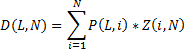
Сразу скажу, что данных о функции Z(i, N) у меня нет. Но можно немного поспекулировать на эту тему.
Единственное, что пришло мне в голову: «20% людей выпивают 80% пива». Возможно, «20% игроков в Hearthstone играют 80% игр»? То есть гипотеза состоит в том, что распределение игроков по количеству сыгранных игр – это дискретное распределение Парето, или, более точно – распределение Ципфа (см. en.wikipedia.org/wiki/Zipf%27s_law).
Введём обозначения:
- Вспомогательная функция
![]()
- Нормировочный множитель (для момента «времени» N)
![]()
Тогда распределение Ципфа со степенным показателем s: 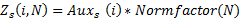
Посмотрим на графики искомой функции D (L,N) в предположении, что распределение игроков по количеству сыгранных игр это распределение Ципфа с показателем степени 1.
Здесь и на следующем графике отображена D (L,N) в моменты «времени» N с 50 до 700.
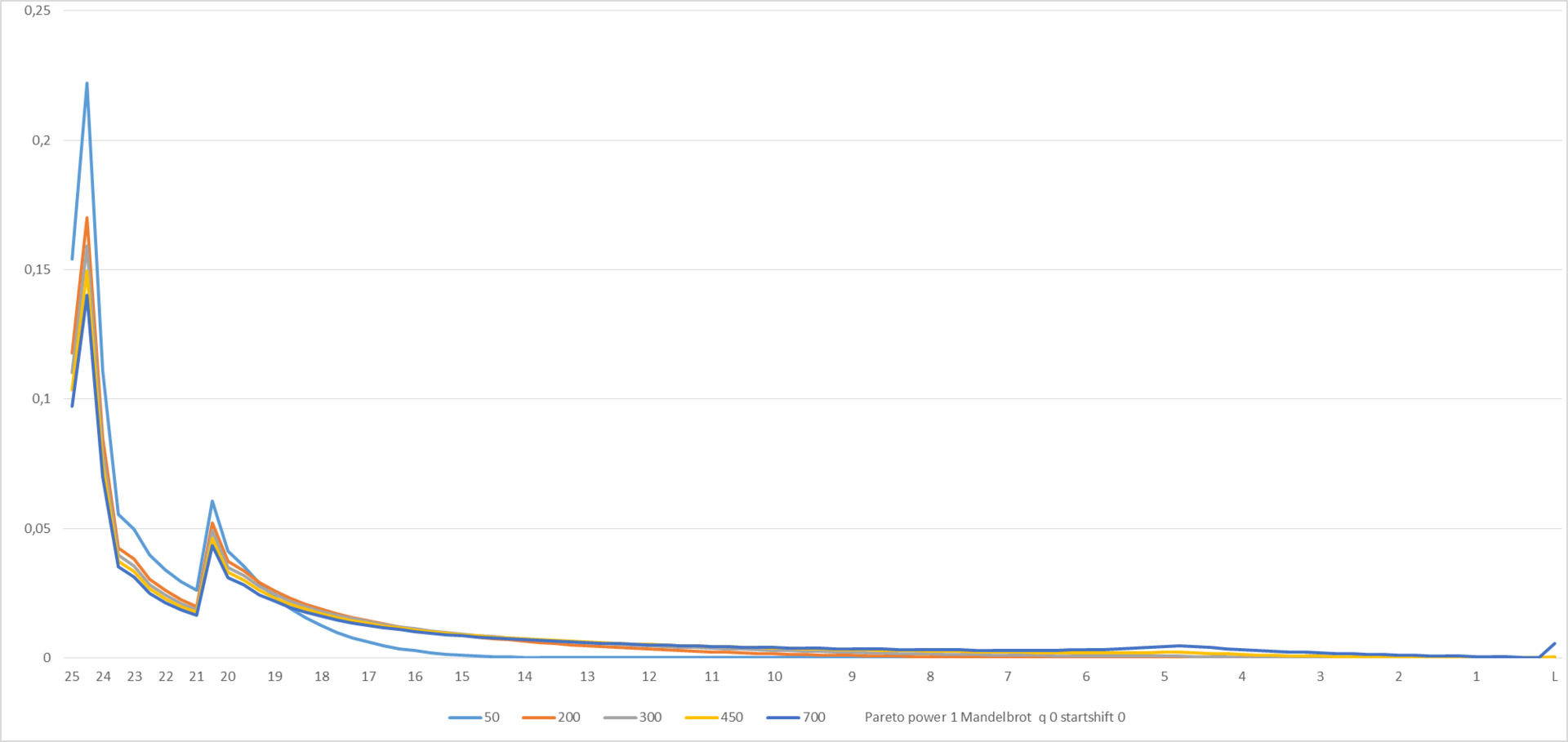
Рисунок 5
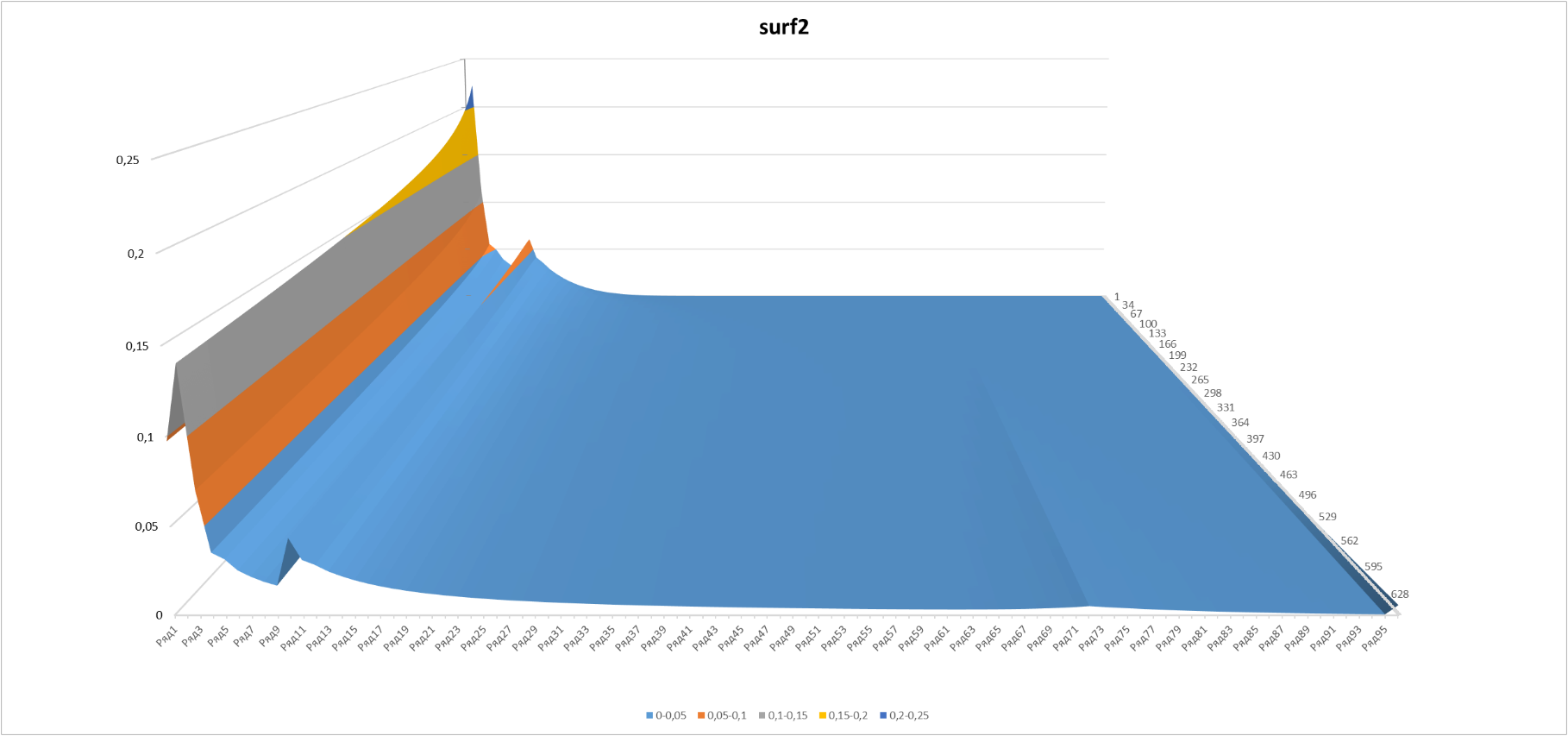
Рисунок 6
Выглядит довольно уродливо, хотя и понятно почему – значительная часть игроков в соответствии с распределением Ципфа осталась на «трамплине». Ну что ж, спекулировать – так по полной. Построим модифицированное распределение Ципфа-Мандельброта (см. en.wikipedia.org/wiki/Zipf%E2%80%93Mandelbrot_law).
1. Заменим вспомогательную функцию
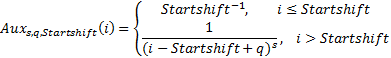
Идея введения целочисленного параметра Startshift состоит в следующем: начало «действия» стандартного поведения распределения Ципфа сдвинуто на Startshift шагов.
Действительно, представляется неправдоподобным, что игрок, прошедший все трудности обучения и только вышедший на рейтинговые игры, с высокой вероятностью бросит играть после одной-двух рейтинговых игр. Можно предположить, что начало «действия» распределения Ципфа примерно совпадает с началом трудностей в продвижении в рейтинге, т.е. с моментом, когда вероятность покинуть «трамплин» превысит ½ (это означает, что startshift=18). Кроме того, из определения вспомогательной функции следует, что общее число игроков «случайно зашедших в Hearthstone» (т.е. сыгравших ≤Startshift игр) совпадает с числом игроков на максимуме распределения. Всё это, конечно, чистая спекуляция, но почему бы не посмотреть, что получится?
Параметр Мандельброта q введён без какого-либо обоснования, на всякий случай.
2. Нормировочный множитель (для момента «времени» N)
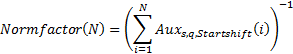
Тогда модифицированное распределение со степенным показателем s, параметром Мандельброта q и параметром «стартового сдвига» Startshift:
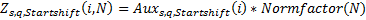
Посмотрим, что получается при параметрах, приведённых в нижней части графика:
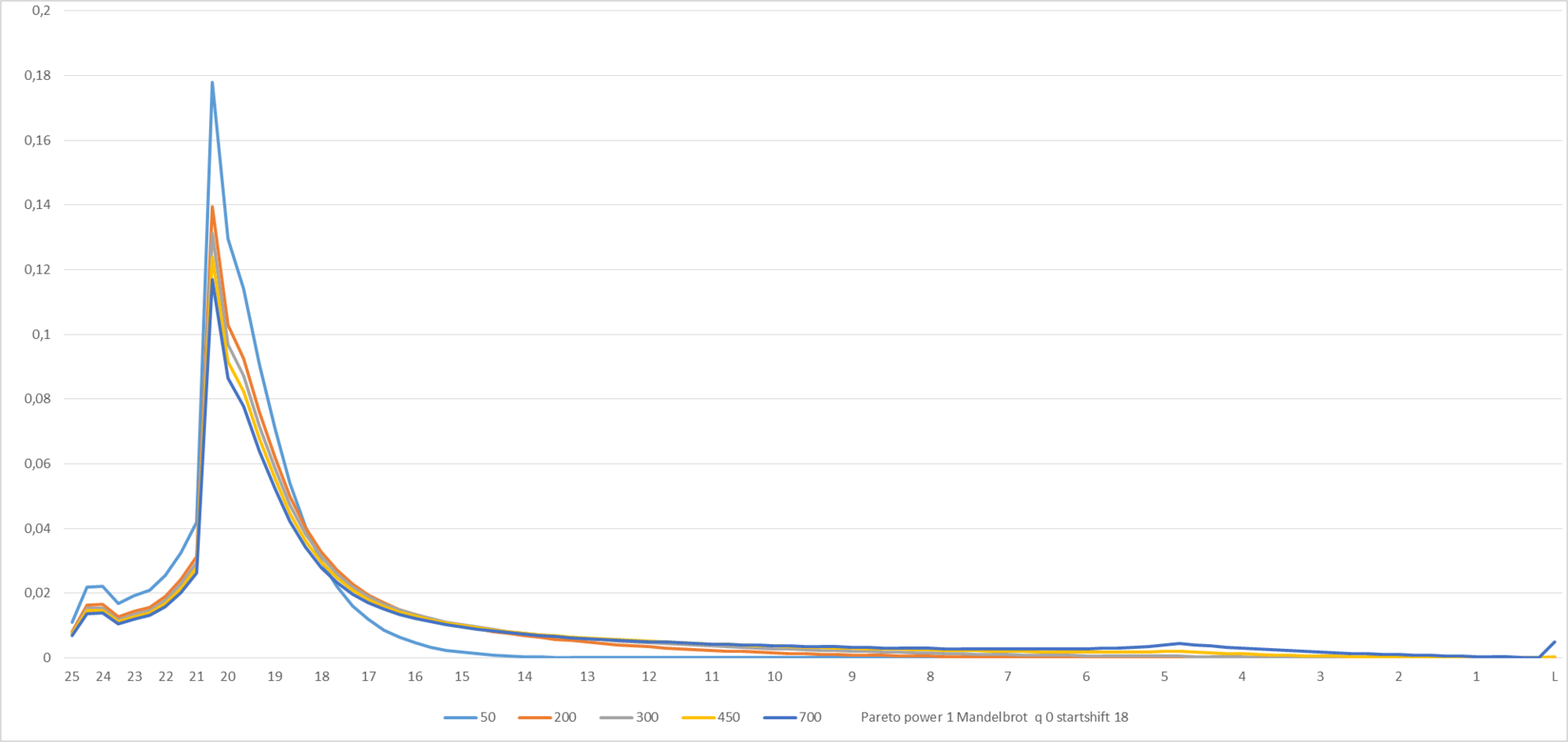
Рисунок 7
Для ручных экспериментов график в Excel сделан интерактивным – можно поиграться с параметрами распределения и отображаемыми «временами» слева от диаграммы на вкладке «Interface», при этом графики (Рисунок 7 и Рисунок 8) будут меняться.
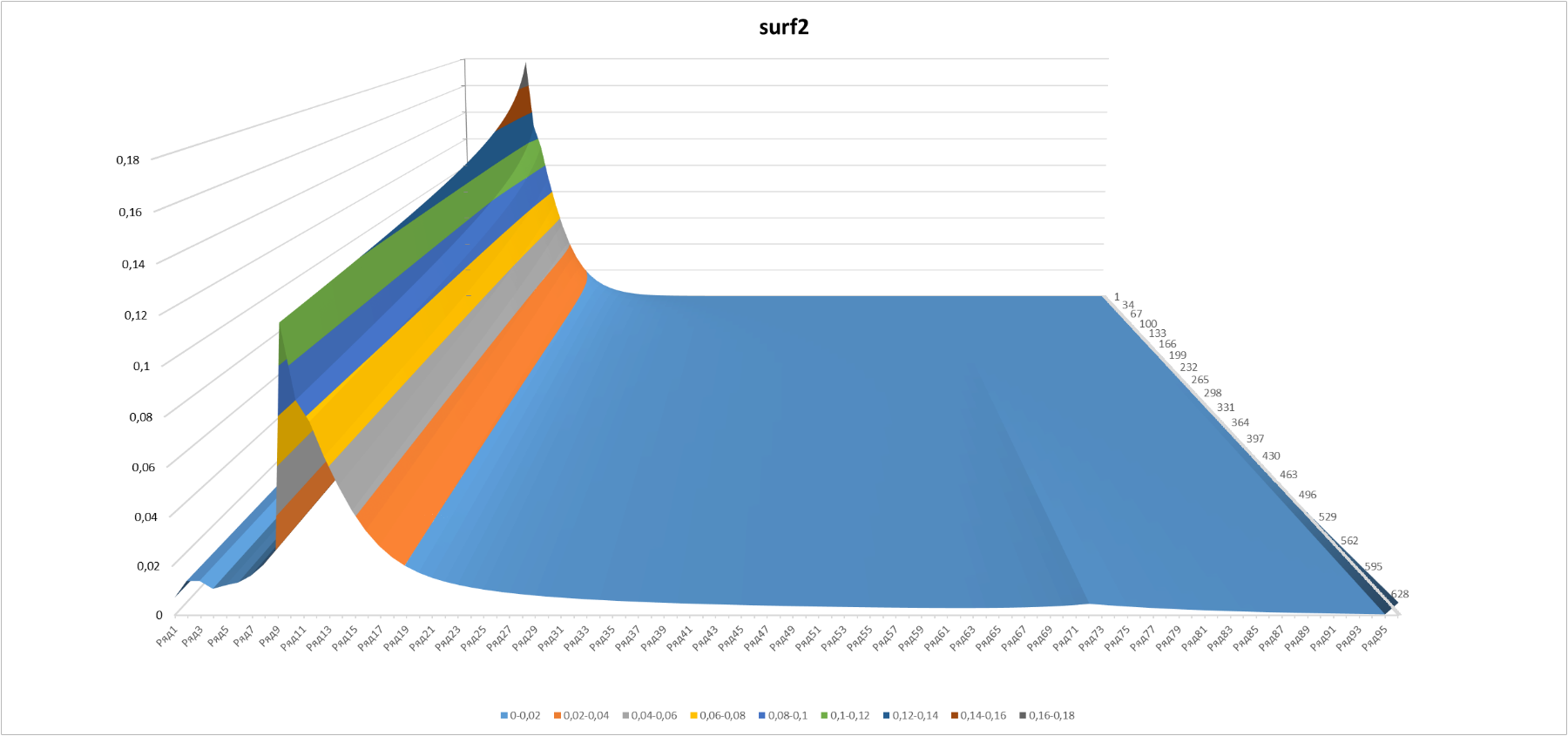
Рисунок 8
И наконец, последний рывок на сегодня. Попробуем подобрать параметры распределения, используя «реальные» данные (http://www.reddit.com/r/hearthstone/comments/23ed7l/how_good_are_you_at_constructed_ladder/). Это результаты какой-то симуляции, детали которой мне неизвестны, неясно, в частности, в какой момент «времени» N проведено измерение и т.д. Это единственное, что я нашёл. Но я не очень старался искать.
Надеюсь, читатели статьи подскажут источник более релевантных данных.
Итерационная обработка данных надстройкой solver и ручная подгонка дали следующие значения параметров распределения: s=1,19; q=0,287; Startshift =110. Startshift ожидаемо большой, поскольку в исходных данных симуляции отсутствует информация о населении уровней 25-21, т.е. «трамплин», очевидно, не симулировался.
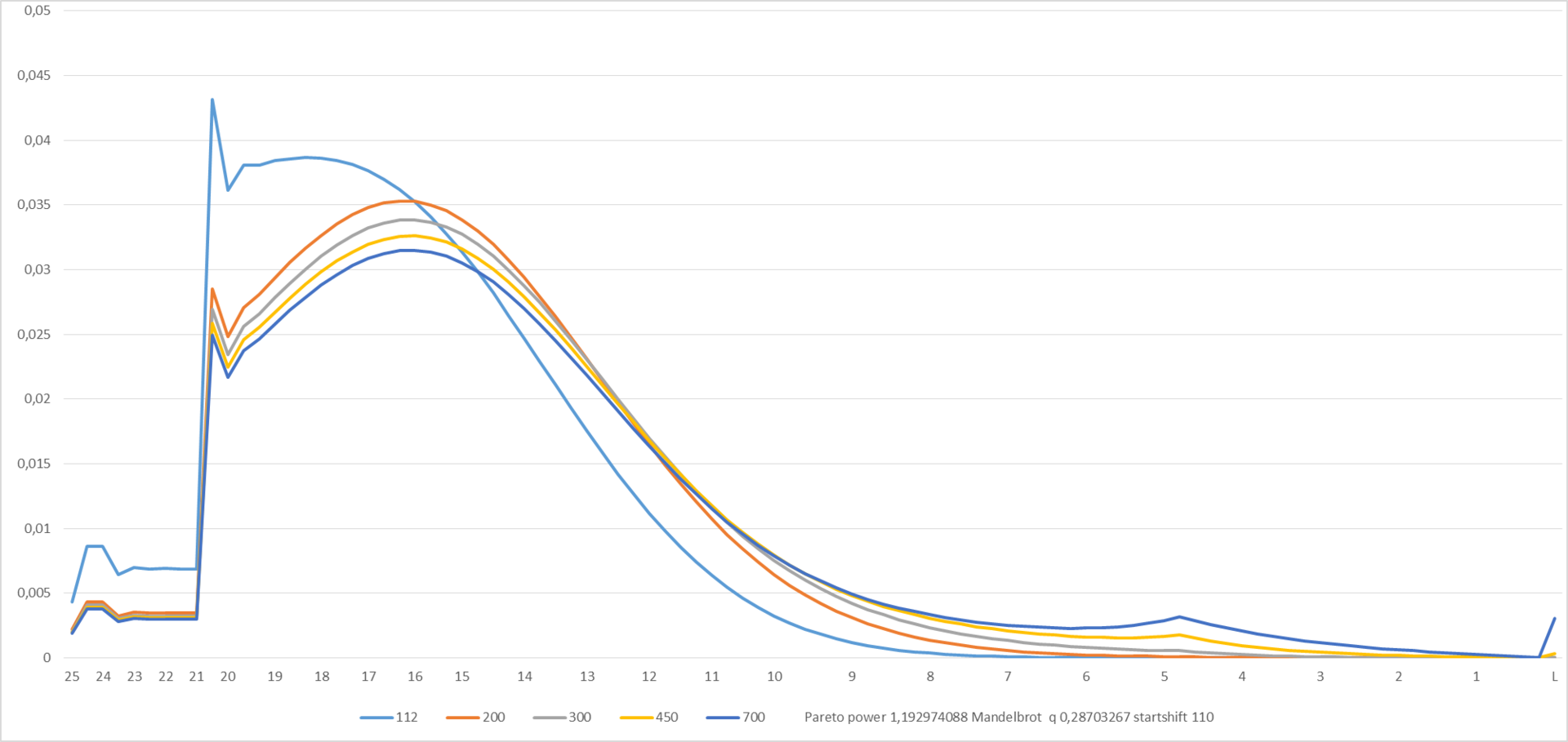
Рисунок 9
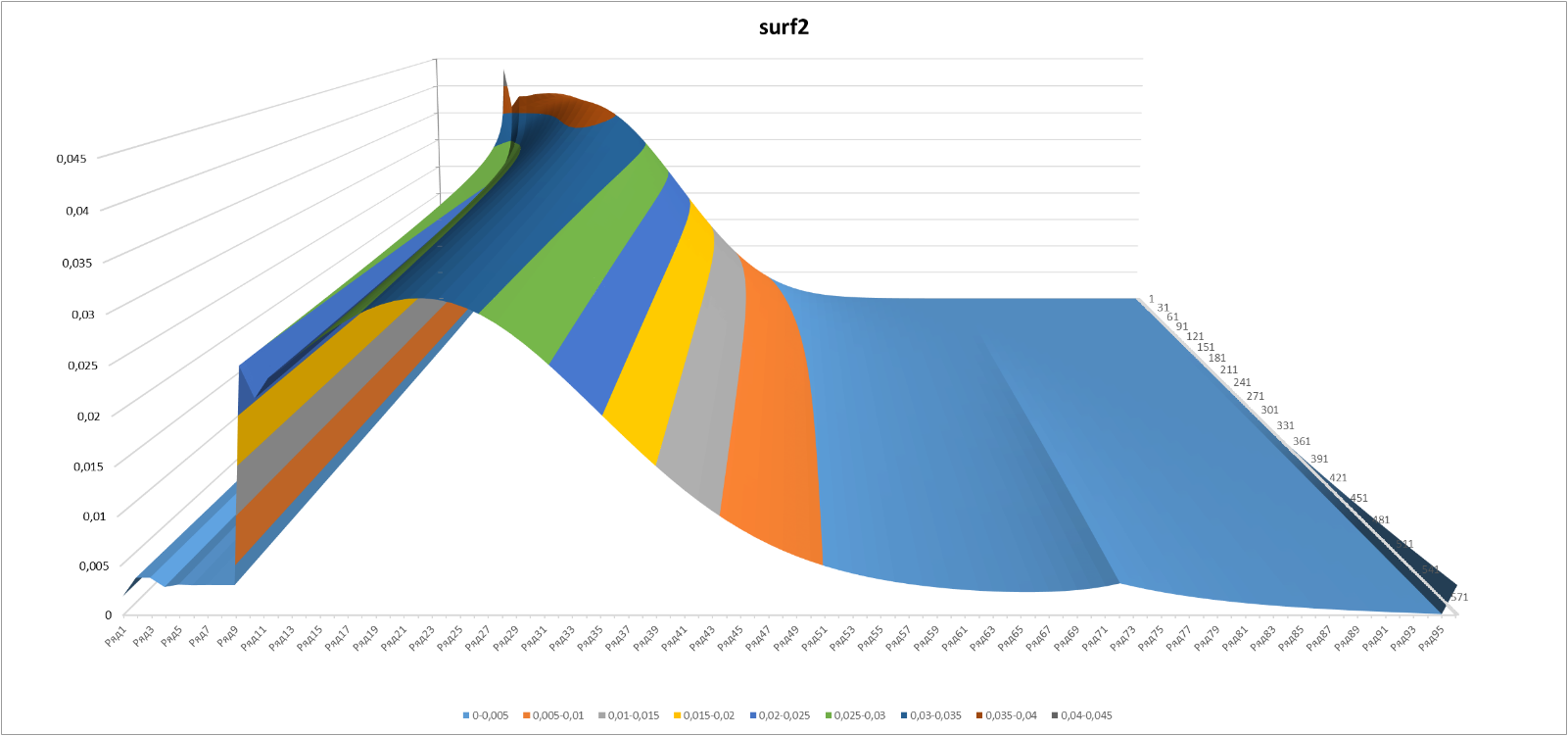
Рисунок 10
Заключение
В заключение повторюсь, что задача, которую я стал решать из чистого любопытства, показалась мне неплохой темой для занятия в школьном математическом кружке. Считаю важным для будущих инженеров и учёных умение использовать для решения внезапно возникающих задач все имеющиеся подручные инструменты: бумагу и карандаш, электронные таблицы, пакет «WOLFRAM MATHEMATICA». Надеюсь, настоящий пример применения электронной таблицы будет кому-нибудь полезен.
При желании преподаватель может проложить мостики от этой задачи ко множеству тем.
Навскидку:
- Теорвер – распределение Парето – Дзета функция – John Derbyshire. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics
- Численные методы решения дифуров в частных производных. (кстати – задача для продвинутых школьников: покажите, что P(L,i) в диапазоне «Нормальная гонка» аппроксимирует некоторое частное решение уравнения
![]() в соответствующем масштабе, а в диапазоне «Гонка с ускорением» — уравнения
в соответствующем масштабе, а в диапазоне «Гонка с ускорением» — уравнения ![]()
- Выбор оптимального для задачи вида функции невязки.
Также можно придумать какие-нибудь расширения к данной задаче. Например, такие:
1) Когда заканчивается сезон, то игроки, достигнувшие определённых уровней в прошлом сезоне, получают некоторую фору. Например, при окончании сезона на уровне 4 игрок получает 21 «звезду», т.е. стартует в новом сезоне не с 25 уровня, а с уровня 17.**- он же 21-й порядковый подуровень (см. Рисунок 1). Уверен, что соответствующие цифры, описывающие зависимость размера форы от достигнутого уровня, легко найти в сети.
- Как изменятся P(L,i) и D (L,N) при учёте форы на старте сезона?
- Сходится ли ряд функций D(L,N, номер сезона) к чему-нибудь при номере сезона, стремящемся к ∞? Если да, то какие ограничения это накладывает на Z (i, N)?
- Достаточно ли Z (i, N) для корректного ответа на 2-й вопрос?
Источник: habr.com
Анонсирован третий сезон турнира StarSeries по Hearthstone

Формат сезона можно назвать традиционным: вся онлайн часть турнира будет сыграна в Стандартном режиме по системе до трех побед с одним баном.
Игры в дивизионе Мир пройдут с 12 по 30 мая. Все 16 приглашенных участников будут разделены на 2 группы, где каждый сыграет с каждым согласно формату round-robin. Два лучших игрока из каждой группы получат путевки на LAN-финал, а игроки, занявшие 3-4 места, перейдут в этап «последнего шанса». Эта часть пройдет в формате двойной сетки плей-офф, а победитель получит последнюю путевку в Киев.
Источник: gameguru.ru
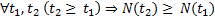 , поэтому N в качестве «времени» вполне годится.
, поэтому N в качестве «времени» вполне годится.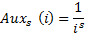
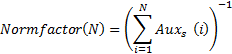
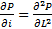 в соответствующем масштабе, а в диапазоне «Гонка с ускорением» — уравнения
в соответствующем масштабе, а в диапазоне «Гонка с ускорением» — уравнения