Всем доброго времени суток! Сегодня мы рассмотрим последние два элемента, которые выполняют простейшие логические функции. Такими элементами являются Исключающее ИЛИ (Exclusive-OR, XOR) и Исключающее ИЛИ-НЕ (None Exclusive-OR, NXOR). Предыдущие статьи смотрите здесь, здесь, здесь и здесь.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Логический элемент Исключающее ИЛИ, как и ранее рассмотренные логические элементы имеет несколько равноправных входов и один выход, но не один из входных выводов не может заблокировать другие входы, установив выходной сигнал к уровню единицы или нуля. Исходя из сказанного, можно установить логику работы элемента Исключающее ИЛИ: высокий логический уровень на выходе появляется только тогда, когда только на одном из входов есть высокий уровень, а если на всех входах одновременно присутствуют сигналы логического нуля или логической единицы, то на выходе буде низкий уровень напряжения. Так же как и все остальные логические элементы элемент Исключающее ИЛИ может иметь инверсию на выходе, такой элемент называют Исключающее ИЛИ-НЕ. Логика работы такого элемента следующая: высокий уровень на выходе логического элемента Исключающее ИЛИ-НЕ появиться только в том случае, когда на всех входах одновременно присутствует сигналы лог. 0 или лог. 1. Таким образом таблица истинности логических элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет иметь следующий вид:
Процессор в MineCraft. Часть 0. Логические элементы и тактовая генерация
| Входные выводы | Тип логического элемента | ||
| 1 | 2 | Исключающее ИЛИ | Исключающее ИЛИ-НЕ |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Элементы Исключающее ИЛИ из-за своего специфического функционала не имеют широкого применения, поэтому отдельных суффиксов в их обозначении не присутствует, они в основном входят в серию ЛП (например, К555ЛП5, КР1533ЛП12, К561ЛП2), в составе которой микросхемы с различным функционалом. Логические элементы Исключающее ИЛИ имеют своё графическое обозначение, которое приведено ниже.
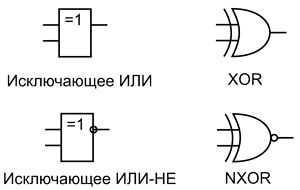
Условное графическое обозначение элементов Исключающее ИЛИ: DIN (слева) и ANSI (справа).
Применение элемента Исключающее ИЛИ
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию суммирования по модулю 2. Поэтому эти элементы иногда называют сумматорами по модулю два. Основное предназначение элементов Исключающее ИЛИ состоит в сравнении двух входных сигналов (когда на входы приходят два высоких или два низких логических уровня на выходе формируется лог. 0), очень часто данный элемент применяют для формирования задержки сигнала или формирования коротких импульсов.
Редстоун мастерская №10 «Логические ячейки»
Управляемый инвертор
Важное применение элементов Исключающее ИЛИ – управляемый инвертор. Опишем его работу. Один из входов используется как управляющий, а на другой поступает сигнал. Если на управляющем входе высокий логический уровень, то сигнал инвертируется, а если низкий, то не инвертируется.
Чаще всего управляющий сигнал задаётся постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
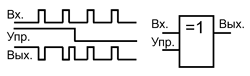
Элемент Исключающее ИЛИ в качестве управляемого инвертора.
Смешивание сигналов
В случае, когда имеется два сигнала и исключается их одновременный приход на элемент Исключающее ИЛИ, то он может быть использован для смешивания сигналов. Такое применение данного элемента может быть использовано в тех случаюх, когда остаются неиспользованными некоторые элементы Исключающее ИЛИ.
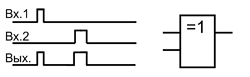
Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов.
Формирование коротких импульсов
Второе важное применение данного элемента – выделение фронта и среза входного импульса, которое традиционно делали с помощью дифференцирующего RC-звена, с последующим усилением и формированием сигнала. Микросхема с элементами Исключающее ИЛИ упрощает данную задачу.
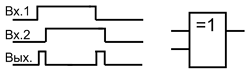
Выделения фронта и среза импульса.
Ниже представлена схема для выделения среза и фронта входящего импульса. Входной сигнал задерживается цепочкой элементов, а затем исходный сигнал и его задержаная копия поступают на входы элемента Исключающее ИЛИ. В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.
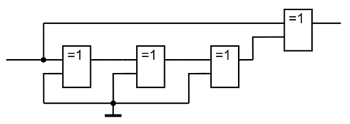
Схема реализующая выделение фронта и среза импульса.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ
Источник: www.electronicsblog.ru
Исключающее или в minecraft
Вентиль строгой дизъюнкции в Minecraft (XOR)
В этом видео я рассказываю о логическом элементе, который реализует операцию исключающее ИЛИ (по другому XOR). У этой операции много названий: логическая неравнозначность, строгая дизъюнкция, поразрядное дополнение, побитовый комплемент.
Вентиль (или гейт) строгой дизъюнкции возвращает на выходе логическую единицу если только на один из входов подана логическая единица.
Кинь денежку на новое оборудование для съемок:
http://goo.gl/TnJ1z5
/files/avatars/av_802442_zC6y.jpg
Источник: goodgame.ru
О битовых операциях
В этой статье я расскажу вам о том, как работают битовые операции. С первого взгляда они могут показаться вам чем-то сложным и бесполезным, но на самом деле это совсем не так. В этом я и попытаюсь вас убедить.
Введение
Побитовые операторы проводят операции непосредственно на битах числа, поэтому числа в примерах будут в двоичной системе счисления.
Я расскажу о следующих побитовых операторах:
- | (Побитовое ИЛИ (OR)),
- > (Побитовый сдвиг вправо).
Битовые операции изучаются в дискретной математике, а также лежат в основе цифровой техники, так как на них основана логика работы логических вентилей — базовых элементов цифровых схем. В дискретной математике, как и в цифровой технике, для описания их работы используются таблицы истинности. Таблицы истинности, как мне кажется, значительно облегчают понимание битовых операций, поэтому я приведу их в этой статье. Их, тем не менее, почти не используют в объяснениях побитовых операторов высокоуровневых языков программирования.
О битовых операторах вам также необходимо знать:
- Некоторые побитовые операторы похожи на операторы, с которыми вы наверняка знакомы (, ||). Это потому, что они на самом деле в чем-то похожи. Тем не менее, путать их ни в коем случае нельзя.
- Большинство битовых операций являются операциями составного присваивания.
Побитовое ИЛИ (OR)
Побитовое ИЛИ действует эквивалентно логическому ИЛИ, но примененному к каждой паре битов двоичного числа. Двоичный разряд результата равен 0 только тогда, когда оба соответствующих бита в равны 0. Во всех других случаях двоичный результат равен 1. То есть, если у нас есть следующая таблица истинности:
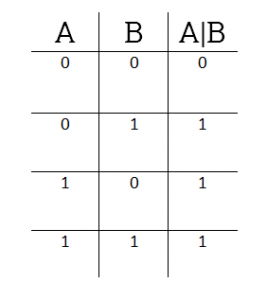
38 | 53 будет таким:
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
В итоге мы получаем 1101112 , или 5510 .
Побитовое И (AND)
Побитовое И — это что-то вроде операции, противоположной побитовому ИЛИ. Двоичный разряд результата равен 1 только тогда, когда оба соответствующих бита операндов равны 1. Другими словами, можно сказать, двоичные разряды получившегося числа — это результат умножения соответствующих битов операнда: 1х1 = 1, 1х0 = 0. Побитовому И соответствует следующая таблица истинности:
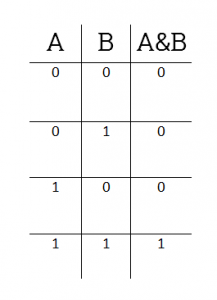
Пример работы побитового И на выражении 38 » border=»1;» width=»500″>
Как результат, получаем 1001002 , или 3610 .
С помощью побитового оператора И можно проверить, является ли число четным или нечетным. Для целых чисел, если младший бит равен 1, то число нечетное (основываясь на преобразовании двоичных чисел в десятичные). Зачем это нужно, если можно просто использовать %2 ? На моем компьютере, например, » border=»1;» width=»500″>
С помощью ^ можно поменять значения двух переменных (имеющих одинаковый тип данных) без использования временной переменной.
Также с помощью исключающего ИЛИ можно зашифровать текст. Для этого нужно лишь итерировать через все символы, и ^ их с символом-ключом. Для более сложного шифра можно использовать строку символов:
String msg = «This is a message»; char[] message = msg.toCharArray(); String key = «.*)»; String encryptedString = new String(); for(int i = 0; i
Исключающее ИЛИ не самый надежный способ шифровки, но его можно сделать частью шифровального алгоритма.
Побитовое отрицание (NOT)
Побитовое отрицание инвертирует все биты операнда. То есть, то что было 1 станет 0, и наоборот.
Вот, например, операция ~52:
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Результатом будет 20310
При использовании побитового отрицания знак результата всегда будет противоположен знаку исходного числа (при работе со знаковыми числами). Почему так происходит, узнаете прямо сейчас.
Дополнительный код
Здесь мне стоит рассказать вам немного о способе представления отрицательных целых чисел в ЭВМ, а именно о дополнительном коде (two’s complement). Не вдаваясь в подробности, он нужен для облегчения арифметики двоичных чисел.
Главное, что вам нужно знать о числах, записанных в дополнительном коде — это то, что старший разряд является знаковым. Если он равен 0, то число положительное и совпадает с представлением этого числа в прямом коде, а если 1 — то оно отрицательное. То есть, 10111101 — отрицательное число, а 01000011 — положительное.
Чтобы преобразовать отрицательное число в дополнительный код, нужно инвертировать все биты числа (то есть, по сути, использовать побитовое отрицание) и добавить к результату 1.
Например, если мы имеем 109:
| A | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| ~A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ~A+1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Представленным выше методом мы получаем -109 в дополнительном коде.
Только что было представлено очень упрощенное объяснение дополнительного кода, и я настоятельно советую вам детальнее изучить эту тему.
Побитовый сдвиг влево
Побитовые сдвиги немного отличаются от рассмотренных ранее битовых операций. Побитовый сдвиг влево сдвигает биты своего операнда на N количество битов влево, начиная с младшего бита. Пустые места после сдвига заполняются нулями. Происходит это так:
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Интересной особенностью сдвига влево на N позиций является то, что это эквивалентно умножению числа на 2 N . Таким образом, 43
Побитовый сдвиг вправо
Как вы могли догадаться, >> сдвигает биты операнда на обозначенное количество битов вправо.
Если операнд положительный, то пустые места заполняются нулями. Если же изначально мы работаем с отрицательным числом, то все пустые места слева заполняются единицами. Это делается для сохранения знака в соответствии с дополнительным кодом, объясненным ранее.
Так как побитовый сдвиг вправо — это операция, противоположная побитовому сдвигу влево, несложно догадаться, что сдвиг числа вправо на N количество позиций также делит это число на 2 N . Опять же, это выполняется намного быстрее обычного деления.
Вывод
Итак, теперь вы знаете больше о битовых операциях и не боитесь их. Могу предположить, что вы не будете использовать >>1 при каждом делении на 2. Тем не менее, битовые операции неплохо иметь в своем арсенале, и теперь вы сможете воспользоваться ими в случае надобности или же ответить на каверзный вопрос на собеседовании.
Источник: tproger.ru