Как построить шестигранник в Майнкрафт

Шаг 1: нарисуйте две параллельные вертикальные линии и горизонтальную линию. Шаг 2: Проведите вертикальную осевую линию и дополнительную горизонтальную линию. Шаг 3: Отметьте точки вдоль средней линии и соедините углы. Шаг 4: Отрезать узор шестиугольной формы по линиям.

Какие формы можно использовать для создания шестиугольника?

Я собрал 2 трапеции сделать шестиугольник. У него 6 сторон и 6 вершин. Он состоит из 2 равных частей.

Как сделать шестиугольник симметричным?

Как нарисовать шестиугольник с двумя линиями симметрии? Шестиугольник имеет шесть линий симметрии. Имея всего два из них, вы легко можете построить треугольник а затем просто повторите это.

Как сделать шестиугольник из ромбов?

Чтобы сделать шестиугольник, вы необходимо использовать ромбы с двумя тупыми и двумя острыми углами. Из бриллиантов с внутренним углом 90 градусов нельзя сделать шестиугольник.

Что такое форма шестиугольника?

Шестиугольник — это Двухмерный геометрический многоугольник с шестью сторонами и шестью углами.. У него нет изогнутых сторон, и все линии замкнуты. Сумма внутренних углов шестиугольника составляет 720º. Есть четыре различных типа шестиугольников.

Как строить простые фигуры в майнкрафте

Источник: alloya.ru

Правильный шестиугольник и его свойства

Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

1. чертится прямая линия и на ней ставится точка;
2. из этой точки строится окружность (она является ее центром);
3. из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
4. после этого отрезками последовательно соединяются все точки на первой окружности.

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Свойства простые и интересные

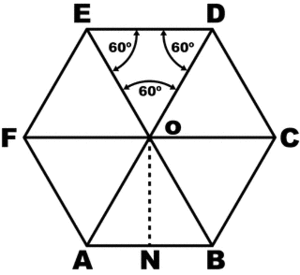
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

1. диаметр описанной окружности;
2. диаметр вписанной окружности;
3. площадь;
4. периметр.

Описанная окружность и возможность построения

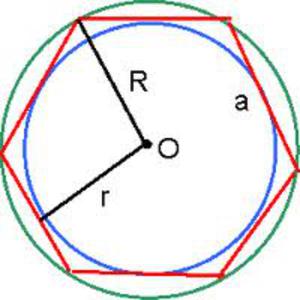
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

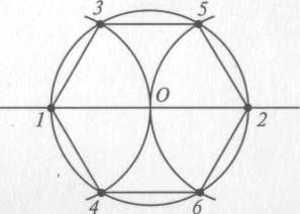
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

1. Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
2. Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
3. Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

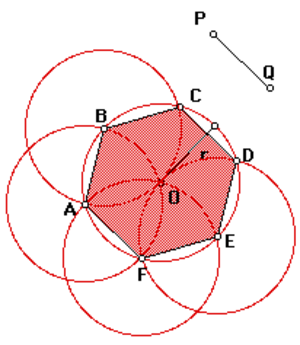
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

1. Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
2. Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
3. Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
4. Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

Площадь нового шестиугольника можно посчитать так:

Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Источник: tokar.guru

Как нарисовать шестиугольник

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 50 человек(а).

Количество просмотров этой статьи: 275 105.

В этой статье:

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Метод 1 из 3:

Рисуем идеальный шестиугольник при помощи циркуля

• Иногда легче сначала нарисовать полкруга в одном направлении, а затем вторую половину — в другом.

Передвиньте иглу циркуля к краю круга. Поставьте ее на вершину круга. Не меняйте угол и расположение циркуля.

Сделайте небольшую отметку карандашом на окружности. Сделайте ее отчетливой, но не слишком темной, так как позже вы ее сотрете. Не забудьте сохранять угол, который вы установили для циркуля.

Переместите иглу циркуля на ту отметку, которую вы только что сделали. Поставьте иглу прямо на отметку.

Сделайте еще одну отметку карандашом на окружности. Таким образом вы сделаете вторую отметку на определенной дистанции от первой отметки. Продолжайте двигаться в одном направлении.

Тем же способом сделайте еще четыре отметки. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.

Соедините отметки при помощи линейки. Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.

Сотрите все вспомогательные линии. Сотрите и круг, и отметки на краях круга, и другие метки, которые вы сделали. Поздравляем — вы нарисовали правильный шестиугольник.

Метод 2 из 3:

Рисуем грубый шестиугольник при помощи круглого предмета и линейки

Обведите ободок стакана карандашом. Таким образом вы нарисуете круг. Очень важно рисовать именно карандашом, так как позже вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутую кружку, банку или что-либо еще, что имеет круглую основу.

Начертите горизонтальные линии через центр круга. Можете воспользоваться линейкой, книгой — чем угодно с прямым краем. Если у вас все же есть линейка, вы можете отметить середину, рассчитав вертикальную длину круга и разделив ее пополам.

Нарисуйте «Х» над половиной круга, разделив его на шесть равных секций. Так как вы уже провели линию через середину круга, «Х» должен быть больше в ширину, чем в высоту, чтобы части были равны. Представьте, что вы делите пиццу на шесть частей.

Сделайте из каждой секции треугольники. При помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, чтобы образовался треугольник. Сделайте это с оставшимися пятью секциями. Представьте, что формируете корочку вокруг кусков пиццы.

Сотрите все вспомогательные линии. К вспомогательным линиям относятся: круг, три линии, которыми круг разделен на секции, и другие отметки, которые вы делали в процессе.

Метод 3 из 3:

Рисуем грубый шестиугольник при помощи одного карандаша

Нарисуйте горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точку горизонтальной линии. Затем поместите карандаш в начальную точку и протягивайте линию к концу. Длина этой линии может составлять лишь несколько сантиметров.

Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа. Представьте, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.

Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь. Таким образом будет создано зеркальное отображение первых двух диагональных линий. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.

Нарисуйте еще одну горизонтальную линию, соединив нижние две диагональные линии. Таким образом вы нарисуете основу шестиугольника. В идеале эта линия должна быть параллельна верхней горизонтальной линии. Вот вы и завершили свой шестиугольник.

Источник: ru.wikihow.com