Как построить угол в Майнкрафте

1й способ. — С помощью «золотого», или «египетского», треугольника. Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град. Этим качеством широко пользовались древние египтяне и другие пракультуры.

• Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров. Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок».
• Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
• Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
• В момент натяжения на линии границы – точка А, вбиваем колышек.
• Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
• После этого натягиваем мерку R5 – от А до В.
• В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника, со сторонами 3;4;5 и с прямым углом в точке О.

2й способ. С помощью циркуля.

Майнкрафт: Как сделать Древесный Уголь

Циркуль может быть веревочный или в виде шагомера. См: …простейший землемерный инструмент

Наш циркуль-шагомер имеет шаг в 1 метр.

Илл.2. Циркуль-шагомер

Построение – также по Илл.1.

• От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
• Ставим ногу циркуля в точку О.
• Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
• Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль.
• Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
• Проводим прямую (отрезок) через точки С и D.
• Все! Полученный отрезок, или прямая, — есть точное направление на север :). Простите, — на прямой угол.
• На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
• Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.

Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля

Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного. Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.

• Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.

Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки

• Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..

Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.

Листочек в клеточку

На листике в клеточку легко можно сделать замеры тех же стандартных углов, что и в предыдущем варианте.

1. Определить 90 градусов будет легче всего – нужно просто нарисовать квадрат.
2. Проведя в квадрате диагональ можно получить угол 45 градусов.
3. Чтобы определить 30, 60 градусов нужно нарисовать прямоугольник (5 клеток в длину, 3 в высоту). Проведя в нем диагональ, получим угол 30 и 60 градусов. Если разделить линией угол 30 на 2 части, получим 15 градусов.

Полученные углы нужно вырезать и сравнить с заданным углом. Обычно, после прикладывания заготовок, получается, визуально определить примерные показатели.

Видео

Как можно вычислить прямой угол?

Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.

Итак, нужно обозначить следующие шаги:

1. Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
2. Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
3. В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
4. После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
5. Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
6. Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
7. В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
8. Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Способы определения разворота

Раньше распространенным решением как вывести угол 90 градусов, например, на фундаменте был обычный строительный уголок. Главное, чтобы он был проверен и соответствовал 90 градусам. Сегодня профессионалы для упрощения процесса и ускорения монтажных работ пользуются лазерными уровнями. Третий вариант – применение обычной измерительной рулетки.

Теорема Пифагора

С этой доказанной теоремой знаком каждый, кто учился в школе. Она применима только к треугольникам, в котором один из углов обязательно прямой. Прилегающие к нему стороны – катеты a и b, соединительный отрезок – гипотенуза (с). Формула выглядит так: a²+b²=c².

Удобство использования такого способа как найти прямой угол при строительстве в том, что наносить разметку можно в любом по площади помещении. Здесь даже допустимо наличие посторонних предметов. Главное, чтобы был доступ к углу и стенам, можно было свободно протянуть соединительную гипотенузу. Дополнительно понадобится только калькулятор, чтобы быстро произвести нужные вычисления.

Египетский треугольник

Золотой или Египетский треугольник – это фигура с прямым углом, у которой стороны равны 3, 4 и 5 частям. Удобство здесь заключается в том, что не нужно возводить параметры в квадратную степень и извлекать корни. Достаточно принять за часть ту или иную условную единицу. Это может быть как 1 см, так и 10 метров, что особенно удобно для решения как вывести угол 90 градусов на стенах из штукатурки.

Если проверить эти утверждения, то гипотенуза или основа равнобедренного треугольника с верхним прямым углом будет при округлении действительно равна 141,4 (141,421356…). С одной стороны – это простой и верный способ как проверить угол 90 градусов рулеткой по нанесенной разметке. Достаточно отмерять метровые участки и сделать только одно умножение 141,4 на число метров. Один только недостаток здесь все же есть. Если в квартире или доме погрешность будет несущественной из-за малых габаритов, то на крупных объектах отклонение из-за неточной гипотенузы может стать заметным.

Коротко главном

В интерьере часто приходится выводить прямые углы под мебель или сантехническое оборудование.

С помощью рулетки можно проверить разворот в 90 градусов тремя способами: стороны равны 3/4/5 частей, если между метровыми стенками соединительный отрезок составляет 141,4 см, применяя теорему Пифагора.

Также рулетки достаточно для формирования трех углов в 30, 45 и 60 градусов.

Дополнительно может понадобиться только калькулятор и карандаш для нанесения разметки.

Источник: 2cheloveka.ru

Как построить угол в Python с помощью Matplotlib?

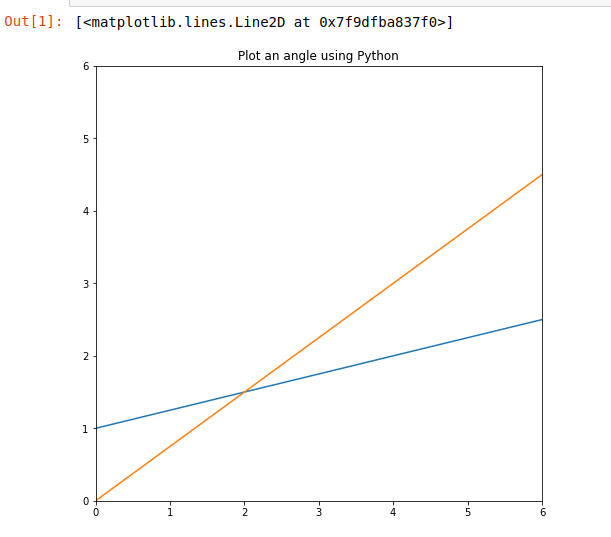
Выход : 2. Найдите точку пересечения и отметьте ее цветом. Здесь x0, y0 обозначают точку пересечения двух прямых. Построенные две Прямые линии записываются как:

у1 = а1 * х + b1 у2 = а2 * х + Ь2.

Решая вышеуказанные уравнения, мы получаем,

х0 = (b2-b1) / (a1-a2) — (i) y0 = a1 * x0 + b1 — (ii)

From above equation (i) and (ii) we will get the point of intersection of Two Straight lines and after that, the color =’midnightblue’ is assigned to the point of intersection using plot.scatter() function.

Python3

# import packages

import matplotlib.pyplot as plt

import numpy as np

# slope and intercepts

a1, b1 = ( 1 / 4 ), 1.0

a2, b2 = ( 3 / 4 ), 0.0

# The numpy.linspace() function returns

# number spaces evenly w.r.t interval

l = np.linspace( — 6 , 6 , 100 )

# use to create new figure

plt.figure(figsize = ( 8 , 8 ))

plt.xlim( 0 , 6 )

plt.ylim( 0 , 6 )

plt.title( «Plot an angle using Python» )

plt.plot(l, l * a1 + b1)

plt.plot(l, l * a2 + b2)

# intersection point

x0 = (b2 — b1) / (a1 — a2)

y0 = a1 * x0 + b1

plt.scatter(x0, y0, color = «midnightblue» )

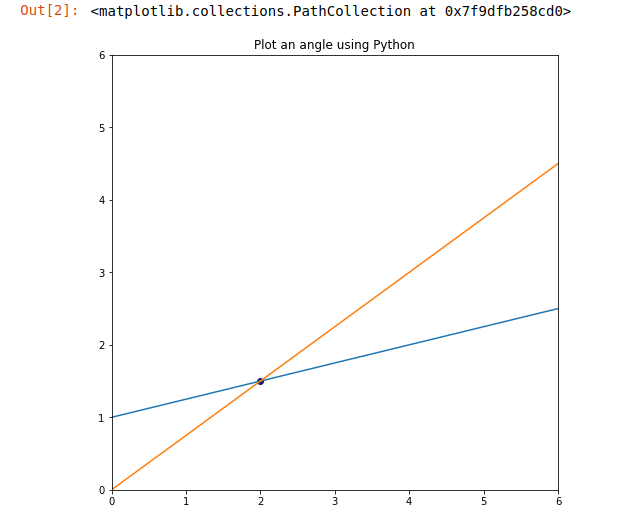
Выход: 3. Постройте окружность так, чтобы точка пересечения двух линий совпадала с центром окружности. Здесь мы строим круг, используя параметрическое уравнение круга. Параметрическое уравнение круга:

x1 = r * cos (тета) х2 = г * грех (тета)

Если мы хотим, чтобы круг не находился в начале координат, мы используем:

х1 = г * соз (тета) + ч х2 = г * грех (тета) + к

Here h and k are the coordinates of the center of the circle. So we use this above equation where h =x0 and k =y0 as shown. Also, here we provide the color to the circle ” blue” and its style is marked as “dotted”.

Python3

# import packages

import matplotlib.pyplot as plt

import numpy as np

# slope and intercepts

a1, b1 = ( 1 / 4 ), 1.0

a2, b2 = ( 3 / 4 ), 0.0

# The numpy.linspace() function returns

# number spaces evenly w.r.t interval

l = np.linspace( — 6 , 6 , 100 )

# use to create new figure

plt.figure(figsize = ( 8 , 8 ))

plt.xlim( 0 , 6 )

plt.ylim( 0 , 6 )

plt.title( «Plot an angle using Python» )

plt.plot(l, l * a1 + b1)

plt.plot(l, l * a2 + b2)

# intersection point

x0 = (b2 — b1) / (a1 — a2)

y0 = a1 * x0 + b1

plt.scatter(x0, y0, color = «midnightblue» )

# circle for angle

theta = np.linspace( 0 , 2 * np.pi, 100 )

x1 = r * np.cos(theta) + x0

x2 = r * np.sin(theta) + y0

plt.plot(x1, x2, color = «green» , linestyle = «dotted» )

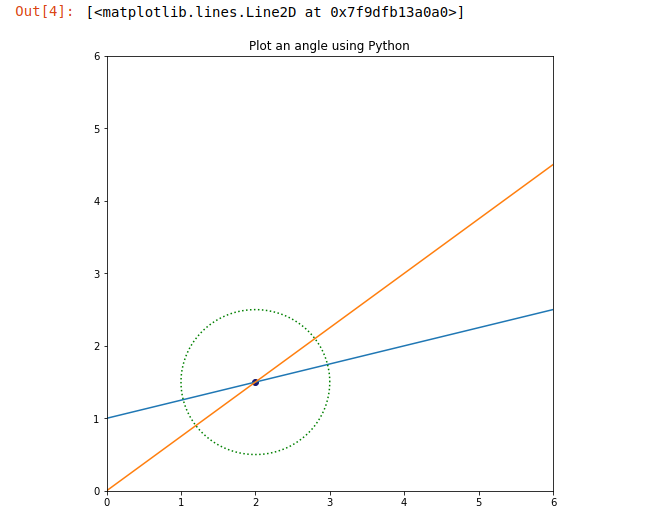
Выход: 4. Отметьте это как точку, где круг будет пересекаться с прямыми линиями, и нанесите эти две точки, где мы найдем угол между ними. Now, let’s find the points where the circle is intersecting the two straight lines. Read the comments below and understand how to mark points. After that color i.e. “crimson” color is provided where the circle will intersect two straight lines.

After that names are provided to the points as Point_P1, Point_P2 where we find the angle between them and marked it as black colored as shown in the output.

Python3

# import packages

import matplotlib.pyplot as plt

Источник: progler.ru

Как построить прямой угол на земле при помощи простейших инструментов?

Можно вывести прямой угол воспользовавшись теоремой Пифагора, на земле надо начертить так называемый «золотой» треугольник.

Соотношение сторон этого треугольника 3:4:5.

Диагональ пять метров.

Не важно в сантиметрах, или миллиметрах, метрах эти размеры, но угол, в этом треугольнике, при этом соотношении всегда будет прямым.

Можно сразу подготовить три верёвки 3-и метра, четыре и пятиметровая, длина верёвки измеряется рулеткой.

Далее вбиваем колышки в землю, на расстоянии друг от друга указанном выше.

Натягиваем верёвку и на финише имеем тот самый прямой угол.

Второй вариант воспользоваться вот таким простеньким строительным угольником,

можно «сколотить» самостоятельно из двух реек.

Далее, если угол в 90-о градусов нужен на большом участке, сбиваем две ровные рейки с углом 90-о градусов, сам угол контролируется угольником.

Нет строительного угольника, можно использовать простенький транспортир.

система выбрала этот ответ лучшим
комментировать
в избранное ссылка отблагодарить
fyodo­ r [4.4K]
6 лет назад

Это — древнейшая геометрическая задача.

Пошаговая инструкция

1й способ. — С помощью «золотого», или «египетского», треугольника. Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град. Этим качеством широко пользовались древние египтяне и другие пракультуры.

Илл.1. Построение Золотого, или египетского треугольника

• Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров. Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок».
• Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
• Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
• В момент натяжения на линии границы – точка А, вбиваем колышек.
• Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
• После этого натягиваем мерку R5 – от А до В.
• В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника, со сторонами 3;4;5 и с прямым углом в точке О.

2й способ. С помощью циркуля.

Циркуль может быть веревочный или в виде шагомера. См: . простейший землемерный инструмент

Наш циркуль-шагомер имеет шаг в 1 метр.

Илл.2. Циркуль-шагомер

Построение – также по Илл.1.

• От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
• Ставим ногу циркуля в точку О.
• Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
• Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль.
• Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
• Проводим прямую (отрезок) через точки С и D.
• Все! Полученный отрезок, или прямая, — есть точное направление на север :). Простите, — на прямой угол.
• На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
• Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.

Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля

Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного. Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.

• Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.

Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки

• Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..

Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.

Источник: www.remotvet.ru