Мод поможет упростить и сократит редстоун схемы при помощи новых микросхем. В Майнкрафт появиться модульный компаратор с возможностью устанавливать в него чипы, которые будут отвечать за алгоритм работы устройства. Чтобы установить чип, возьмите его в руку и нажмите правую кнопку мыши в пустую рамку компаратора.
Скриншоты
Как установить Logic Chips?
- Установите Minecraft Forge
- Нажмите Win+R (кнопка «Win» находиться между «Ctrl» и «Alt»)
- В появившемся окне напишите %appdata%
- Перейдите в .minecraft/mods (если нету папки «mods», то создайте)
- Перетащите мод (.zip/.jar) в папку mods
Источник: minecraftexpert.ru
Элементы схемотехники. Логические схемы
Процессор в MineCraft. Часть 0. Логические элементы и тактовая генерация
Любое устройство компьютера, выполняющее арифметические или логические операции, может рассматриваться как преобразователь двоичной информации: значения входных переменных для него — последовательность нулей и единиц, а значение выходной функции — новая двоичная последовательность. Необходимые преобразования информации в блоках компьютера производятся логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.
В комбинационной схеме набор выходных сигналов в любой момент времени полностью определяется набором входных сигналов.
В цифровых автоматах с памятью набор выходных сигналов зависит не только от набора входных сигналов, но и от внутреннего состояния данного устройства. Такие устройства всегда имеют память.
Схемотехника — научно-техническое направление, занимающееся проектированием, созданием и отладкой электронных схем и электронных устройств различного назначения.
21.1. Логические элементы
Логический элемент — это устройство с л входами и одним выходом, которое преобразует входные двоичные сигналы в двоичный сигнал на выходе.
Работу любого логического элемента математически удобно описать как логическую функцию, которая упорядоченному набору из нулей и единиц ставит в соответствие значение, также равное нулю или единице.
В схемотехнике широко используются логические элементы, представленные в таблице 4.2.
Таблица 4.2
Условные обозначения типовых логических элементов
Логический элемент И (конъюнктор) реализует операцию логического умножения. Единица на выходе этого элемента появится тогда и только тогда, когда на всех входах будут единицы.
Базовые компоненты редстоун схем. Redstone guides #1 Логические элементы, регистры, декодер и т д
Опишите подобным образом логические элементы ИЛИ (дизъюнктор), НЕ (инвертор), И-НЕ, ИЛИ-НЕ.
Однотипность сигналов на входах и выходах позволяет подавать сигнал, вырабатываемый одним элементом, на вход другого элемента. Это позволяет из двухвходовых элементов «собирать» многовходовые элементы (рис 4.7), а также синтезировать произвольные комбинационные схемы, соединяя в цепочки отдельные логические элементы.
Рис. 4.7. Схема и обозначение четырёхвходового конъюнктора
Пример. По заданной логической функции F(A, В) =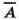 
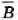построим комбинационную схему (рис. 4.8).
Построение начнём с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).
Рис. 4.8. Комбинационная схема функции F(A, В) =
21.2. Сумматор
Из отдельных логических элементов можно составить устройства, производящие арифметические операции над двоичными числами.
Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.
Вспомним схему сложения двух n-разрядных двоичных чисел (рис. 4.9).
Рис. 4.9. Схема сложения двух n-разрядных двоичных чисел
Заметим, что при сложении цифр в i-м разряде мы должны сложить цифру ai числа а, цифру bi числа b, а также рi — перенос из (i — 1)-го разряда. В результате сложения должны получиться цифра результата si и цифра переноса (0 или 1) в следующий разряд pi+1.
Основываясь на этих рассуждениях, построим таблицу истинности для функций, которые в зависимости от цифр ai, bi и pi получают цифры si и pi+l.
Вам известен алгоритм построения логического выражения по таблице истинности. Воспользуемся им и запишем выражение для функции pi+1:
Попытаемся упростить это выражение, воспользовавшись тем, что A v А = А. Основываясь на этом законе, включим в имеющуюся дизъюнкцию ещё два слагаемых вида ai pi, причём на основании коммутативного и ассоциативного законов преобразуем полученное выражение к виду:
Полученное выражение означает, что функция рi+1 принимает значение 1 только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Обратите внимание на то, что такой вывод можно сделать и в результате анализа таблицы истинности.
По таблице истинности можем записать выражение для si:
Его также можно попытаться преобразовать к более короткому виду. Но можно пойти другим путём и провести более тщательный анализ таблицы истинности для функции si.
Из таблицы видно, что значение si равно 1, если все входные сигналы равны 1. Этому соответствует выражение ai pi = 1.
Или значение si равно 1, если в комбинации входных сигналов есть единственная 1, т. е. единица среди переменных есть, но нет одновременно двух переменных, значения которых равны
1. Это можно записать так:
Следовательно, s,- можно записать так:
Можно попытаться самостоятельно провести преобразование логического выражения, полученного по таблице истинности для si к итоговому виду. Но, чтобы убедиться в равносильности этих двух выражений, достаточно построить таблицу истинности для второго из них.
Полученные выражения позволяют реализовать одноразрядный двоичный сумматор схемой, представленной на рисунке 4.10.
Рис. 4.10. Схема одноразрядного сумматора
Выразить si и pi+1 можно и другими формулами. Например, самое короткое выражение для si имеет вид: si = ai ? bi ? pi, что позволяет построить сумматор, используя другие логические элементы.
Сложение n-разрядных двоичных чисел осуществляется с помощью комбинации одноразрядных сумматоров (условное обозначение одноразрядных сумматоров приведено на рисунке слева).
21.3. Триггер
Триггер (от англ. trigger — защёлка, спусковой крючок) — логический элемент, способный хранить один разряд двоичного числа.
Триггер был изобретён в 1918 году М. А. Бонч-Бруевичем.
Самый простой триггер — RS. Он состоит из двух логических элементов ИЛИ-HE, входы и выходы которых соединены кольцом: выход первого соединён со входом второго и выход второго — со входом первого. Схема RS-триггера представлена на рисунке 4.11.
Рис. 4.11. Логическая схема RS-триггера
Триггер имеет два входа: S (от англ. set — установка) и R (от англ. reset — сброс) и два выхода: Q (прямой) и (инверсный). Принцип его работы иллюстрирует следующая таблица истинности:
Если на входы поступают сигналы R = 0 и S = O, то триггер находится в режиме хранения — на выходах Q и сохраняются установленные ранее значения.
Если на установочный вход S на короткое время поступает сигнал 1, то триггер переходит в состояние 1 и после того, как сигнал на входе S станет равен 0, триггер будет сохранять это состояние, т. е. будет хранить 1.
При подаче 1 на вход R триггер перейдёт в состояние 0.
Подача на оба входа S и R логической единицы может привести к неоднозначному результату, поэтому такая комбинация входных сигналов запрещена.
Триггер используется для хранения информации в оперативной памяти компьютера, а также во внутренних регистрах процессора. Для хранения одного байта информации необходимо 8 триггеров, для килобайта — 8 • 1024 триггеров. Оперативная память современных компьютеров содержит миллионы триггеров.
В целом же компьютер состоит из огромного числа логических устройств, образующих все его узлы и память.
САМОЕ ГЛАВНОЕ
Необходимые преобразования информации в блоках компьютера производятся логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.
В комбинационной схеме набор выходных сигналов в любой момент времени полностью определяется набором входных сигналов. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом. Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.
В цифровых автоматах с памятью набор выходных сигналов зависит не только от набора входных сигналов, но и от внутреннего состояния данного устройства. Такие устройства всегда имеют память. Триггер — логический элемент, способный хранить один разряд двоичного числа. Оперативная память современных компьютеров содержит миллионы триггеров.
В целом же компьютер состоит из огромного числа логических устройств, образующих все его узлы и память.
Источник: murnik.ru
Построение логических элементов
Логические схемы — схемы, состоящие из логических элементов. Они используются при построении вычислительных устройств для обеспечения выполнения арифметических, логических и других операций над машинными словами.
В основе метода построения и анализа логических схем лежит аппарат алгебры логики.
Основные, или базовые, логические элементы производят по планарной технологии с использованием резисторов, диодов и транзисторов.
При этом различают элементы: резисторно-транзисторной логики (РТЛ); диодно-транзисторной логики (ДТЛ); транзисторно-транзисторной логики (ТТЛ); транзисторной логики (ТЛ).
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
| Элементарные логические операции над двоичными переменными реализуются схемами, которые называются логическими элементами. Число входов логического элемента соответствует числу аргументов воспроизводимой им булевой функции. |
| Логическая функция реализуется логическим элементом ИЛИ (дизъюнктором) и изображается на схемах в следующем виде: |
| Логическая функция f(x1, x2, …, xn) = x1 x2 … xn реализуется логическим элементом И (конъюнктором): |
| Логическая функция реализуется логическим элементом НЕ (инвертором): |
| Cхему, показывающую связи между различными логическими элементами, где сами элементы представлены условными обозначениями, называют логической (более корректно — функциональной) схемой. |
| Набор элементов для построения логической схемы является функционально полным, если реализуемые этими элементами булевы функции образуют функционально полную систему функций, т.е. с их помощью можно выразить любые другие логические функции. Дизъюнктор, конъюнктор и инвертор образуют функционально полный набор. |
| Сформулируем основные требования к логическим элементам вычислительных устройств. Высокое быстродействие. Суть этого требования вполне ясна, так как именно быстродействие элементов определяет в конечном счете быстродействие вычислительной машины. Для логических элементов существенную роль в этом отношении играет время переключения. Достаточно большая нагрузочная способность. Нагрузочная способность определяет число других элементов, которые можно подключать к выходу данного элемента, сохраняя нормальные условия его работы. Высокая помехоустойчивость. Логические элементы должны быть устойчивы к помехам, которые всегда присутствуют в электрических цепях, — ложные сигналы, вызванные наводками от параллельных цепей, шумы вследствие случайных флуктуаций зарядов в физических элементах и т.п. Малая потребляемая мощность. Потребляемая элементами мощность рассеивается, главным образом, в виде тепла. Большое тепловыделение нарушает режимы работы схем и ограничивает элементов, что ведет к увеличению размеров элементов, а значит, и машины в целом. Как можно меньшее количество физических элементов. Схемы, требующие меньшего количества физических элементов, оказываются эффективнее как с экономической точки зрения, так и с точки зрения надежности и долговечности. |
ЭЛЕКТРИЧЕСКИЕ СИГНАЛЫ — ФИЗИЧЕСКИЕ АНАЛОГИ ДВОИЧНЫХ ЦИФР
| Физическими аналогами двоичных цифр в вычислительных устройствах служат электрические сигналы в соответствующих точках схем, способные принимать два хорошо различимых значения. Напрмер, можно использовать: высокий уровень напряжения схемы (5 В) как логическую единицу — 1, низкий (0 В) — как логический нуль — 0; ферромагнитное колечко намагничено в одном направлении — 1, в другом — 0; наличие импульса тока — 1, отсутствие — 0. | |
| В схемах цифровых устройств эти сигналы изменяются и воспринимаются не непрерывно, а в некоторые дискретные моменты времени. Временной интервал между этими моментами называется тактом. Цифровые устройства обычно содержат специальный блок — блок синхронизации, вырабатывающий синхронизирующие сигналы, следующие через равные интервалы времени и отмечающие указанные моменты. | |
| Понятие такта позволяет разграничить два способа представления информации в цифровой вычислительной машине: потенциальный и импульсный. При потенциальном способе цифрам 0 и 1 соответствуют высокий и низкий уровень напряжения в данной точке; потенциальным называется сигнал, меняющий свою величину один раз за такт. При импульсном способе цифрам 0 и 1 соответствует, например, отсутствие и наличие импульса; импульсом называется сигнал, изменяющий свою величину дважды в течение такта. На рис.2.1 показано изменение напряжения при потенциальном и импульсном изображениях одного и того же слова 100010111. |
ЭЛЕКТРИЧЕСКИЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
| Используя представление двоичных цифр электрическими сигналами, мы можем на простейших электронных схемах получить реализацию трех базовых логических операций. |
| Самым простым электрическим логическим элементом с двумя устойчивыми состояниями является переключатель, который может быть замкнут или разомкнут. В первых цифровых вычислительных машинах в качестве переключателей использовались электромеханические реле (рис.2.2). |
| На рис.2.2,а изображен электрический логический элемент И. Наличие напряжений Ux1 или Ux2, равных 5В, приводит к замыканию контактов реле. Логическая единица на выходе устройства (Uy = 5В) возникает в случае Ux1 = Ux2 = 5B , в других случаях Uy = 0 . |
| Электрический логический элемент ИЛИ на двух реле представлен на рис.2.2,б. Наличие хотя бы одного из сигналов Ux1 или Ux2, равного 5В, приводит к замыканию контактов одного из реле и Uy = 5В (логическая 1). |
| Элемент НЕ состоит из одного реле (рис.2.2,в). Наличие Ux = 5В приводит к замыканию контактов реле и Uy = 0В. |
Источник: rustaste.ru